Descriptive Statistics

 

The three most important descriptive statistics are:

·         Measures of central tendency - which describe the typical (average) score (or value) in a set of data. These are mean, median and mode.

·         Measures of variability - which describe the spread or dispersion among the scores in a set of data. These are the range and standard deviation

·         Correlation coefficients - which describe relationships between variables.

 Tabular and Graphical Presentation of Data

This section introduces tabular and graphical methods commonly used to summarize both categorical and quantitative data. Tabular and graphical summaries of data can be found in annual reports, newspaper articles, and research studies.

1.       Presentation of Qualitative Data

Example

The data below is from 20 people who bought soft drinks at a grocery on a particular day. The soft drinks are Coke, Fanta and Sprite.

Table 1. Data for Soft Drinks

Coke	Sprite	Fanta	Coke
Fanta	Coke	Sprite	Coke
Coke	Coke	Sprite	Coke
Sprite	Fanta	Sprite	Fanta
Sprite	Coke	Coke	Fanta

We note that this data is categorical and it can be measured using a nominal scale ofmeasurement. The descriptive tools to summarise this type of data include, fequency distribution, the Bar Chart and a Pie Chart.

2.       Frequency Distribution

A frequency distribution is a tabular summary that shows non-overlapping classes or intervals of data entries with a count of the number of entries in each class. The frequency of a class is the number of data entries in the class.

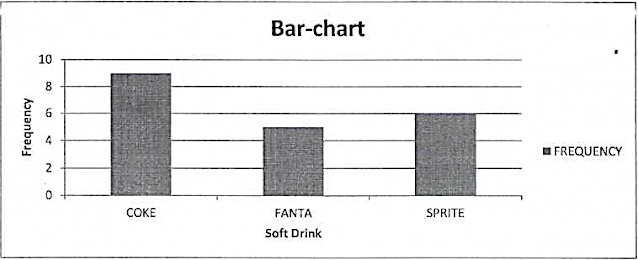
Table 2: Frequency Distribution Table for Soft Drinks

SOFT DRINK	FREQUENCY	RELATIVE FREQUENCY	PERCENT FREQUENCY
COKE	9	0.45	45
FANTA	5	0.25	25
SPRITE	6	0.3	30
TOTAL	20	1	100

From the table, we can infer that Coke was the most purchased brand of soft drink followed by Sprite, and Fanta was purchased the least.

The Relative Frequency of a class equals the fraction or proportion of items belonging to a class.

A relative frequency distribution gives a tabular summary of data showing the relative frequency for each class.

Relative frequency=(Frequency of Class)/(Total number of Observation)

The Percent Frequency of a class is the relative frequency multiplied by 100. A percent frequency distribution summarizes the percent frequency of the data for each class.

3.       Bar Chart

A bar chart (bar graph) is a graphical device for depicting categorical data summarized in a frequency, relative frequency, or percent frequency distribution. Each category in the frequency distribution is represented by a bar or rectangle, and the picture is constructed in such a way that the area of each bar is proportional to the corresponding frequency or relative frequency.

To construct a bar chart we mark the various categories on the horizontal axis and frequencies on the vertical axis. All categories are represented by intervals of the same width and we draw one bar for each category such that the height of the bar represents the frequency of the corresponding category. We leave a small gap between adjacent bars.

In quality control applications, bar charts are used to identify the most important causes of problems. When the bars are arranged in descending order of height from left to right with the most frequently occurring cause appearing first, the bar chart is called a Pareto diagram. This diagram is named for its founder, Vilfredo Pareto, an Italian Economist.

The bar graphs for relative frequency and percentage distributions can be drawn simply by marking the relative frequencies or percentages, instead of the frequencies, on the vertical axis.

4.       Pie Chart

A circle divided into portions that represent the relative frequencies or percentages of a population or a sample belonging to different categories is called a Pie Chart. A pie chart is more commonly used to display percentages, although it can be used to display frequencies or relative frequencies. The whole pie (or circle) represents the total sample or population. Then we divide the pie into different portions that represent the different categories.

As we know, a circle contains 360 degrees. To construct a pie chart, we multiply 360 by the relative frequency of each category to obtain the degree measure or size of the angle for the corresponding category. For example, the category "very" occupies 0.33×360=119 degrees of a circle.

Presentation of Quantitative Data

1.    Frequency distribution

As defined earlier, a frequency distribution is a description of a variable providing a count of the number of cases that fall into each of the variable’s categories. There are two types of frequency distributions, thus; ungrouped frequency distribution and grouped frequency distribution.

2.    Ungrouped frequency distribution

This distribution where the number of times the observation occurs appears separately. Consider the following set of data which are the Ages of 30 members of the women's club. We wish to summarize this data by creating a frequency distribution of the ages.

Table 3: Data set for ages of 30 women

50	45	49	50	43
49	50	49	45	49
47	47	44	51	51
44	47	46	50	44
51	49	43	43	49
45	46	45	51	46

To create a frequency distribution from this data we proceed as follows:

(i)     Identify the highest and lowest values in the data set. For our Age of women data the oldest is 51 and the youngest is 43.

(ii)   Create a column with the title of the variable we are using, in this case Age. Enter the highest score at the top, and include all values within the range from the highest score to the lowest score.

(iii) Create a tally column to keep track of the scores as you enter them into the frequency distribution. Once the frequency distribution is completed you can omit this column.

(iv)  Create a frequency column, with the frequency of each value, as show in the tally column, recorded.

(v)    The relative frequency and percent frequency can be calculated and presented as we did for categorical data.

(vi)  At the bottom of the frequency column record the total frequency for the distribution

(vii)       Enter the name of the frequency distribution at the top of the table.

If we applied these steps to the age data, we would have the following frequency distribution.

Table 4: Frequency Distribution for age of women

Age	Tally	Frequency	Cumulative Frequency	Relative Frequency	Percentage Frequency
43	///	3	3	0.1	10
44	///	3	6	0.1	10
45	////	4	10	0.13	13.33
46	///	3	13	0.1	10
47	///	3	16	0.1	10
48		0	16	0	0
49	//////	6	22	0.2	20
50	////	4	26	0.13	13.33
51	////	4	30	0.13	13.33
Totals		30		1	100

3.       Cumulative Frequency Distribution

Cumulative frequency can be defined as the sum of all previous frequencies up to the current point.

The cumulative frequency is calculated by adding each frequency from a frequency distribution table to the sum of its predecessors.

The last value will always be equal to the total for all observations, since all frequencies will already have been added to the previous total.

The cumulative frequency for a given value can also be obtained by adding the frequency for the value to the cumulative value for the value below the given value. For example the cumulative frequency for 45 is 10 which is the cumulative frequency for 44 (6) plus the frequency for 45 (4). In summary then, to create a cumulative frequency distribution:

(i)     Create a frequency distribution and add a column entitled cumulative frequency

(ii)   The cumulative frequency for each score is the frequency up to and including the frequency for that score.

(iii) The highest cumulative frequency should equal N (total of the frequency column).

The Relative Frequency of a class equals the fraction or proportion of items belonging to a class as defined for categorical data. A relative frequency distribution gives a tabular summary of data showing the relative frequency for each class. For example, the relative frequency of the women aged 45 is 0.133.

Relative frequency=(Frequency of Class)/(Total number of Observations)

The Percent Frequency of a class is the relative frequency multiplied by 100. A percent frequency distribution summarizes the percent frequency of the data for each class. For example, the percentage frequency of the women aged 45 is 13.3%.

1.       Grouped frequency distribution

This is where the number of times items appear is grouped and given a range. In some cases, it is necessary to group the values of the data to summarize the data properly.

For example, you wish to create a frequency distribution for the IQ scores in your class of 30 pupils. The IQ scores in your class range from 73 to 139. To include these scores in a frequency distribution you would need 67 different score values (73 up to 139). This would not summarize the data very much. To solve this problem we would group scores and create a grouped frequency distribution.

Another example where data is usually reported as grouped frequencies is age. This is convenient if we want to make general statements about certain age groups such as the youth, young or the aged.

(a)             Guidelines for Creating Class Intervals

Although we are not following these strict guidelines in creating class intervals for grouped frequency distributions, you may wish to know what they are helpful.

(i)     Determine the number of non-overlapping classes: There should be approximately 5 to 20 mutually exclusive class intervals. "Mutually exclusive" means that a score can belong to only one class interval. Two non-mutually exclusive class intervals would be 45-49 and 47- 51 since the scores 47, 48, and 49 could belong to either class interval

(ii)   Determine the width (size) of each class: The size of the class interval can also be determined based on the required number of class intervals. This can be estimated as: 

Approximate class size=Range/(Required number of class intervals)

Where the range is defined as Largest data value -Smallest data value. The class interval size should be equal for all class intervals

(iii)   Determine the class limits:

-          Lower Class Limit: Identifies the smallest possible data value assigned to a class. The lower limit of each class interval should be a multiple of the class interval size.

-          Upper class Limit: Identifies the largest possible data value assigned to a class.

-          Stated Limits: these are the given limits. They are also known as empirical limits because they are the ones that the researcher creates based on their best judgement For example,if you state the class as 10-14, this will encampass the lowest value of 12 as given in table 3.5. Since the stated limits make sure that classes are mutually exclusive, they might omit some values such as 14.5.

-          True Limits: This is theoretically the lowest or highest value that can be assigned to an interval. They are found by adding 0.5 to the stated upper limit and subtracting 0.5 from the stated lower limit of a class. In the above example, the true limits would be 10.5-14.5.

-          The size of the class interval is the difference between the True Upper Limit and the True Lower Limit.

(b)   Reasons for computing True Limits

-          Avoidance of gaps between the class intervals when dealing with continuous data, such as weight, age, height, temperature and so on.

-          Avoidance of ambiguity when assigning cases to ensure mutual exclusivity of classes.

-          Ensure accuracy in computing certain statistics measures such as the median, mode, mean, and measures of variability.

(c)     Concept of the class Mid-Point

The class Mid-Point is simply the middle value of a particular class interval. It is calculated as Mid-point=(True Lower Limit+True Lower limit)/2. It is important to calculate the Class Mid-Point because it is needed to calculate the numerical measures of grouped data such as the Mean. It is also used in the construction of the Frequency Polygon.

Example 3

Consider the age of 20 members of the Small Christian Community who participated in voting for the church leadership. We wish to summarize this data by creating a frequency distribution of the age.

Table 5: Data set for ages of 20 members of St. John’s Small Christian Community

12	19	14	18
15	18	15	17
20	22	27	23
22	33	21	28
14	16	18	13

(i)     Number of classes: Specify the number of classes that will be used to group the data. Since the recommended is 5-20 classes, we can choose the minimum of five since our sample is small.

(ii)   Size of the classes: using the formula, the approximate class size is: 

Approximate class size=Range/(Required number of class intervals)=(33-12)/5≈4

(ii)Class Limits: As stated above, we choose the class limits in such a way that data belong to one and only one class. Since 12 is the smallest value, it should be included in the first class interval and 33 is the largest value and should be included in the last class. In this example, we can start with 10 as our Lower Class Limit of the first class. With a class size of 5, the classes would be 10-14,15-19, 20-24, 25-29,30-34.

Table 6: Grouped Frequency for ages of 20 members of St. John's Small Christian Community

Age Group	Midpoint(x)	f	rf	%f	cf	rcf	%cf
10-14	12	4	0.2	20	4	0.2	20
15-19	17	8	0.4	40	12	0.6	60
20-24	22	5	0.25	25	17	0.85	85
25-29	27	2	0.1	10	19	0.95	95
30-34	32	1	0.05	5	20	1	100
Grand Total		20	1	100

 Class Mid-point=(True Lower Limit+True Lower limit)/2=(9.5+14.5)/2=12

for the first class. We add the class size to the preceding midpoint to get the rest.

-          Relative frequency and percent frequency are calculated as demonstrated in the example for ungrouped data.

-          The cumulative frequency column shows the number of data items with values less than or equal to the upper class limit of each class as defined earlier. For example, 17 members or 85% are below or equal to 24 years old.

 Graphical Presentation of Quantitative Data

Histogram

-          A histogram is similar to the common bar graph but it is used to represent data at the interval or ratio level of measurement.

-          The histogram can be constructed for data previously summarized as either a frequency, relative frequency or percent frequency distribution.

-          There is need to convert the class limits into true class limits since the data is continuous.

-          Using the above data we have the following histogram.

Figure 3: Histogram showing forages of 20 members of St John's Small Christian Community

2.    Frequency Polygon

A frequency polygon is a curve resulting from plotting the class mid-points on the x-axis and the frequency on the y-axis. It helps us determine the shape of distribution for the data. Another way of drawing the frequency polygon is by superimposing the line on the top centre of each bar of the histogram. Using the data for members of the Small Christian Community above;

3.  Cumulative Frequency Curve (Ogive Curve)

Cumulative frequencies of a distribution can also be plotted as a graph. The curve that results by plotting these is called the Ogive Curve. Since the cumulative frequencies can either be 'less than’ or ‘more than’ type, there are two type of Ogives called 'less than' type and 'more than' type Ogive. The value of median and other partition values can be located from the ogives.

Less than Ogive: The less than cumulative frequencies are in ascending order. The cumulative frequency of each class is plotted against the upper limit of the class interval in this type of ogive and then various points are joined by straight line.

More than Ogive: The cumulative frequencies in this type are in the descending order. The cumulative frequency of each class is plotted against the lower limit of the class interval.

Less than Cumulative Distribution Curve for Age of 20 members

4.  Dot Plot

This is a graph where the horizontal axis shows the range of the data and each value is represented by a dot above the axis.

If we use the data for ages of 20 members of St. John’s Small Christian Community; we have the following Dot-Plot.